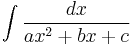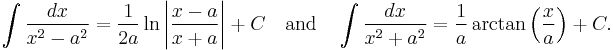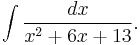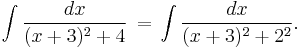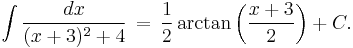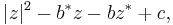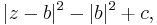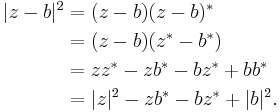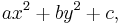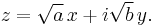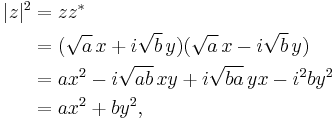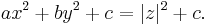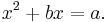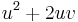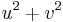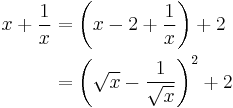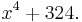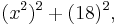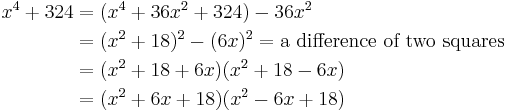Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form
to the form
In this context, "constant" means not depending on x. The expression inside the parenthesis is of the form (x − constant). Thus one converts ax2 + bx + c to
and one must find h and k.
Completing the square is used in
- solving quadratic equations,
- graphing quadratic functions,
- evaluating integrals in calculus,
- finding Laplace transforms.
In mathematics, completing the square is considered a basic algebraic operation, and is often applied without remark in any computation involving quadratic polynomials.
Contents |
Overview
Background
There is a simple formula in elementary algebra for computing the square of a binomial:
For example:
In any perfect square, the number p is always half the coefficient of x, and the constant term is equal to p2.
Basic example
Consider the following quadratic polynomial:
This quadratic is not a perfect square, since 28 is not the square of 5:
However, it is possible to write the original quadratic as the sum of this square and a constant:
This is called completing the square.
General description
Given any monic quadratic
it is possible to form a square that has the same first two terms:
This square differs from the original quadratic only in the value of the constant term. Therefore, we can write
where k is a constant. This operation is known as completing the square. For example:
Non-monic case
Given a quadratic polynomial of the form
it is possible to factor out the coefficient a, and then complete the square for the resulting monic polynomial.
Example:
This allows us to write any quadratic polynomial in the form
Formula
The result of completing the square may be written as a formula. For the general case:[1]
Specifically, when a=1:
Relation to the graph
In analytic geometry, the graph of any quadratic function is a parabola in the xy-plane. Given a quadratic polynomial of the form
the numbers h and k may be interpreted as the Cartesian coordinates of the vertex of the parabola. That is, h is the x-coordinate of the axis of symmetry, and k is the minimum value (or maximum value, if a < 0) of the quadratic function.
In other words, the graph of the function ƒ(x) = x2 is a parabola whose vertex is at the origin (0, 0). Therefore, the graph of the function ƒ(x − h) = (x − h)2 is a parabola shifted to the right by h whose vertex is at (h, 0), as shown in the top figure. In contrast, the graph of the function ƒ(x) + k = x2 + k is a parabola shifted upward by k whose vertex is at (0, k), as shown in the center figure. Combining both horizontal and vertical shifts yields ƒ(x − h) + k = (x − h)2 + k is a parabola shifted to the right by h and upward by k whose vertex is at (h, k), as shown in the bottom figure.
Solving quadratic equations
Completing the square may be used to solve any quadratic equation. For example:
The first step is to complete the square:
Next we solve for the squared term:
Then either
and therefore
This can be applied to any quadratic equation. When the x2 has a coefficient other than 1, the first step is to divide out the equation by this coefficient: for an example see the non-monic case below.
Irrational and complex roots
Unlike methods involving factoring the equation, which is only reliable if the roots are rational, completing the square will find the roots of a quadratic equation even when those roots are irrational or complex. For example, consider the equation
Completing the square gives
so
Then either
so
In terser language:
Equations with complex roots can be handled in the same way. For example:
Non-monic case
For an equation involving a non-monic quadratic, the first step to solving them is to divide through by the coefficient of x2. For example:
Other applications
Integration
Completing the square may be used to evaluate any integral of the form
using the basic integrals
For example, consider the integral
Completing the square in the denominator gives:
This can now be evaluated by using the substitution u = x + 3, which yields
Complex numbers
Consider the expression
where z and b are complex numbers, z* and b* are the complex conjugates of z and b, respectively, and c is a real number. Using the identity |u|2 = uu* we can rewrite this as
which is clearly a real quantity. This is because
As another example, the expression
where a, b, c, x, and y are real numbers, with a > 0 and b > 0, may be expressed in terms of the square of the absolute value of a complex number. Define
Then
so
Geometric perspective
Consider completing the square for the equation
Since x2 represents the area of a square with side of length x, and bx represents the area of a rectangle with sides b and x, the process of completing the square can be viewed as visual manipulation of rectangles.
Simple attempts to combine the x2 and the bx rectangles into a larger square result in a missing corner. The term (b/2)2 added to each side of the above equation is precisely the area of the missing corner, whence derives the terminology "completing the square". [1]
A variation on the technique
As conventionally taught, completing the square consists of adding the third term, v 2 to
to get a square. There are also cases in which one can add the middle term, either 2uv or −2uv, to
to get a square.
Example: the sum of a positive number and its reciprocal
By writing
we show that the sum of a positive number x and its reciprocal is always greater than or equal to 2. The square of a real expression is always greater than or equal to zero, which gives the stated bound; and here we achieve 2 just when x is 1, causing the square to vanish.
Example: factoring a simple quartic polynomial
Consider the problem of factoring the polynomial
This is
so the middle term is 2(x2)(18) = 36x2. Thus we get
(the last line being added merely to follow the convention of decreasing degrees of terms).
References
- ^ Narasimhan, Revathi (2008). Precalculus: Building Concepts and Connections. Cengage Learning. p. 133–134. ISBN 0-618-41301-4. http://books.google.com/books?id=hLZz3xcP0SAC., Section Formula for the Vertex of a Quadratic Function, page 133–134, figure 2.4.8
- Algebra 1, Glencoe, ISBN 0-07-825083-8, pages 539–544
- Algebra 2, Saxon, ISBN 0-939798-62-X, pages 214–214, 241–242, 256–257, 398–401
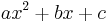
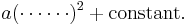
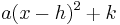
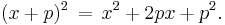
![\begin{alignat}{2}
(x%2B3)^2 \,&=\, x^2 %2B 6x %2B 9 && (p=3)\\[3pt]
(x-5)^2 \,&=\, x^2 - 10x %2B 25\qquad && (p=-5).
\end{alignat}](/2012-wikipedia_en_all_nopic_01_2012/I/146b17914932579724035c471f364829.png)
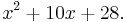
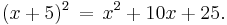
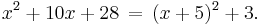
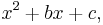
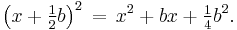
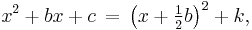
![\begin{alignat}{1}
x^2 %2B 6x %2B 11 \,&=\, (x%2B3)^2 %2B 2 \\[3pt]
x^2 %2B 14x %2B 30 \,&=\, (x%2B7)^2 - 19 \\[3pt]
x^2 - 2x %2B 7 \,&=\, (x-1)^2 %2B 6.
\end{alignat}](/2012-wikipedia_en_all_nopic_01_2012/I/40ae53053680564f116c71828dc0461c.png)
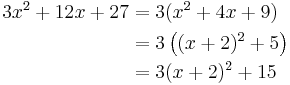
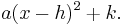
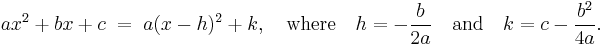
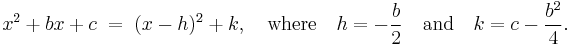
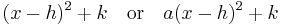
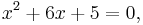
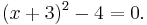
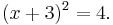
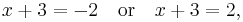
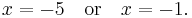
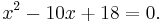
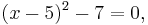
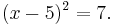
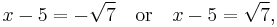
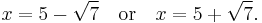
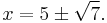
![\begin{array}{c}
x^2 %2B 4x %2B 5 \,=\, 0 \\[6pt]
(x%2B2)^2 %2B 1 \,=\, 0 \\[6pt]
(x%2B2)^2 \,=\, -1 \\[6pt]
x%2B2 \,=\, \pm i \\[6pt]
x \,=\, -2 \pm i.
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/c185a2c292b0f2c0f818df01a1e20164.png)
![\begin{array}{c}
2x^2 %2B 7x %2B 6 \,=\, 0 \\[6pt]
x^2 %2B \tfrac{7}{2}x %2B 3 \,=\, 0 \\[6pt]
\left(x%2B\tfrac{7}{4}\right)^2 - \tfrac{1}{16} \,=\, 0 \\[6pt]
\left(x%2B\tfrac{7}{4}\right)^2 \,=\, \tfrac{1}{16} \\[6pt]
x%2B\tfrac{7}{4} = \tfrac{1}{4} \quad\text{or}\quad x%2B\tfrac{7}{4} = -\tfrac{1}{4} \\[6pt]
x = -\tfrac{3}{2} \quad\text{or}\quad x = -2.
\end{array}](/2012-wikipedia_en_all_nopic_01_2012/I/498b8dae2e67b9bea6433a9cb156e835.png)